기초 기호 표 (Elementary Symbol Table)
I. 기호 표 (Symbol Table)
기호 표 (Symbol table)는 추상적 개념에 연산을 추가하기 위해 고안된 자료구조로, 컴파일러 또는 인터프리터와 같은 언어 변환기에서 사용하고 있습니다.
이번 강의에서는 기호 표 자료구조를 위한 메서드와, 구현 방법에 대해 알아보겠습니다.
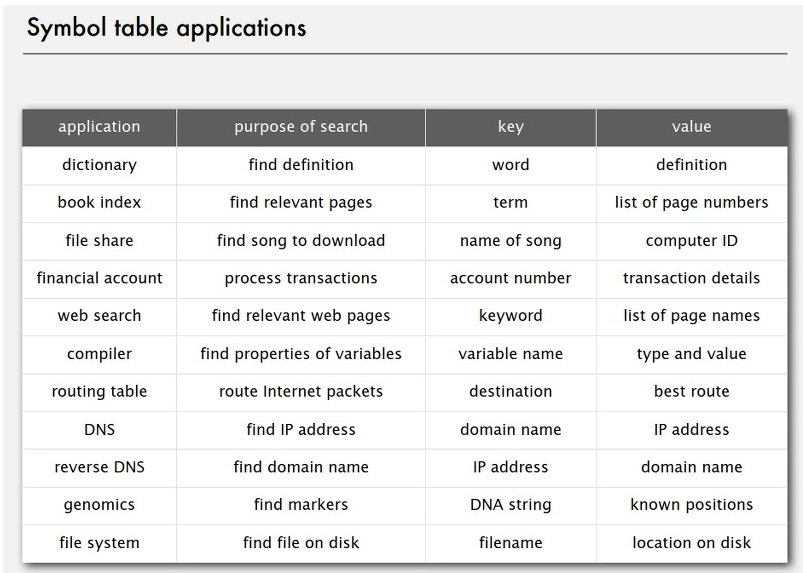
I-1. Basic symbol table API
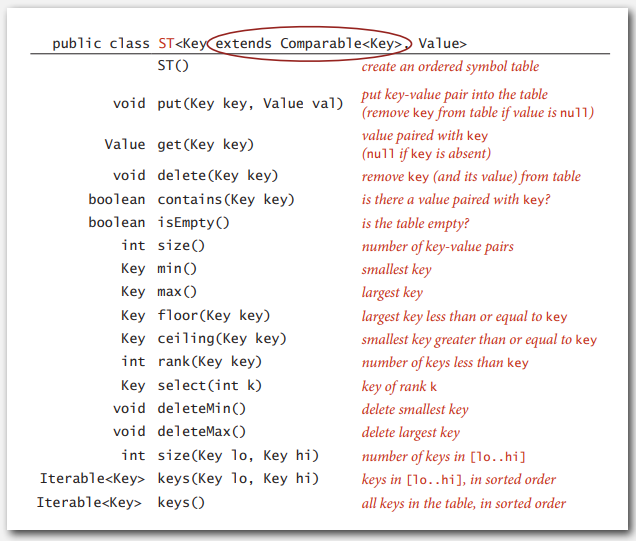
기호 표의 기본 메서드는 다음과 같습니다.
- key와 value 저장하기 -
void put (key, value) - 주어진 key로 value 검색하기 -
value get (key) - 주어진 key로 value 삭제하기 -
void delete (key) - 모든 key 내용 불러오기 -
Iterable<key> keys()
I-2. Conventions
이러한 기호 표 자료구조는 몇가지 관습 (conventions)을 가집니다.
- value는
null이 아니어야 한다 get()을 호출했을 때 key값에 대응되는 value가 없으면null을 반환한다put()을 호출하여 새로운 value를 저장하면 overwrite된다
I-3. Keys and values
key에 몇가지를 조건을 추가하면 기호 표를 유용하게 사용할 수도 있습니다. value에는 어떠한 자료형도 사용해도 문제 없습니다.
- key가
compareTo()로 비교할 수 있는 Comparable인 경우 - key가
equals()연산을 지원하는 경우 - key가
hashCode()연산을 지원하는 경우
I-4. Equality test
equals() 메서드는 두 객체를 동일한 객체로 판단할 것인지 알려주는 기능을 수행합니다. 그러면 두 객체가 동일한 객체인지 어떻게 알 수 있을까요?
- Reflexive: x.equals(x)가 항상 참이고
- Symmetric: y.equals(x)와 x.equals(y)가 필요 충분 조건이고
- Transitive: x.equals(y)가 참이고, y.equals(z)가 참이면
- x.equals(z)는 참이다 (x=y=z는 동치 관계)
1-5. 사용자 정의 클래스의 equals 구현하기
#include <iostream>
using namespace std;
class Time {
private:
int hour, min, sec;
public:
Time() = default;
~Time() = default;
Time(int h, int m, int s) : hour(h), min(m), sec(s) {}
bool operator==(const Time& T) const {
return (hour == T.hour && min == T.min && sec == T.sec);
}
};
int main() {
Time A(1, 2, 3);
Time B(2, 3, 4);
if(A==B) {
cout << "A is same with B" << endl;
} else {
cout << "A is different from B" << endl;
}
}II. Elementary Implementations
기호 표를 구현하기 위한 두 가지 방법에 대한 내용을 설명합니다. 구현 방법은 다르지만 두 방법 모두 자료를 검색할 때는 equals() 메서드를 사용해야 합니다.
- 자료를 입력 순서대로 저장하는 방법
- 자료를 항상 정렬해서 저장하는 방법
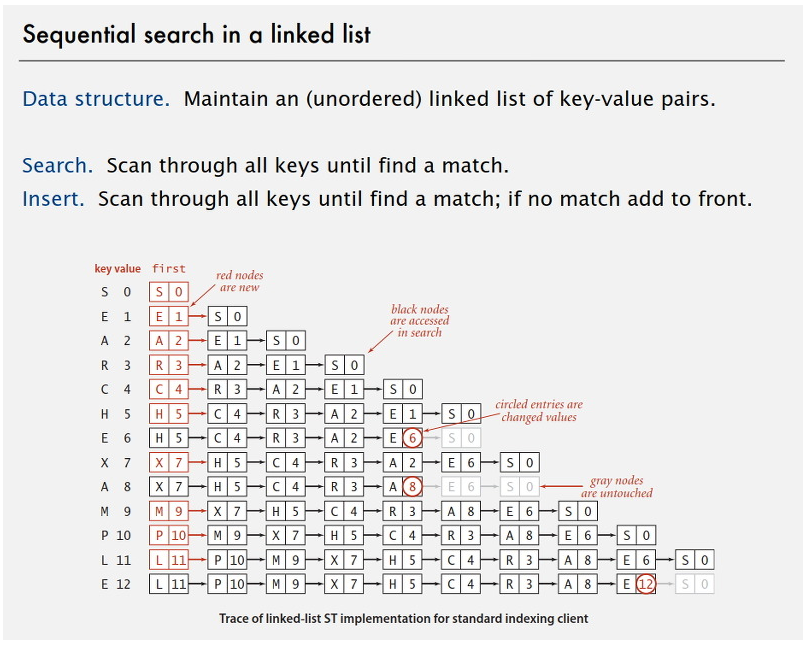
II-1. 연속된 연결 리스트 사용하기
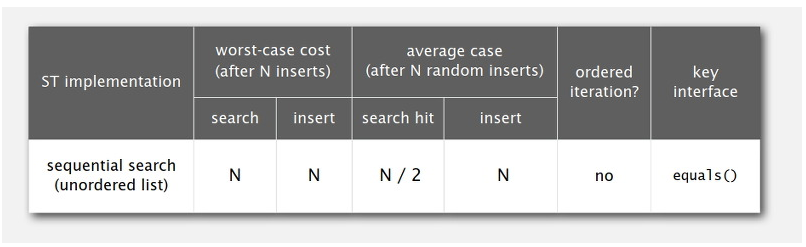
가장 단순한 방법은 연결 리스트에 자료를 저장하고 자료를 앞에서부터 차례대로 검색하는 방법입니다.
- 자료 구조: key-value 쌍을 갖는 연결 리스트 e.g.)
vector<pair<int, string>> v; - 검색: key가 일치하는 key-value 쌍이 나올 때까지 순차적으로 검색
- 삽입: key가 일치하는 key-value 쌍이 있으면 overwrite하고 없으면 추가
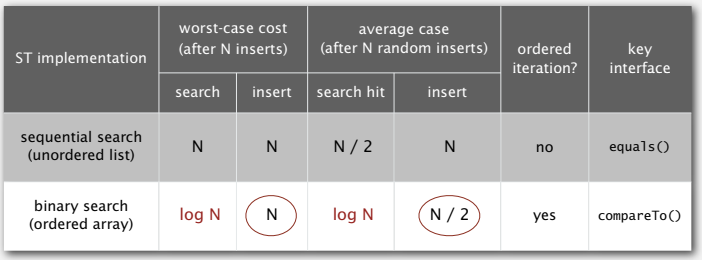
II-2. 이진 탐색으로 정렬하기
이진 탐색은 데이터가 정렬되어 있는 배열에서 값을 찾아내는 알고리즘입니다.
- 배열의 중간 값
m을 선택하여 찾으려고 하는x와 비교한다 x ≤ m이면 좌측의 데이터를 기준으로 다시 탐색한다x > m이면 우측의 데이터를 기준으로 다시 탐색한다- 값을 찾을 때까지 반복한다
아래 그림은 keys[] 배열에서 P와 Q를 찾을 때 이진 탐색이 수행되는 과정을 보여줍니다.
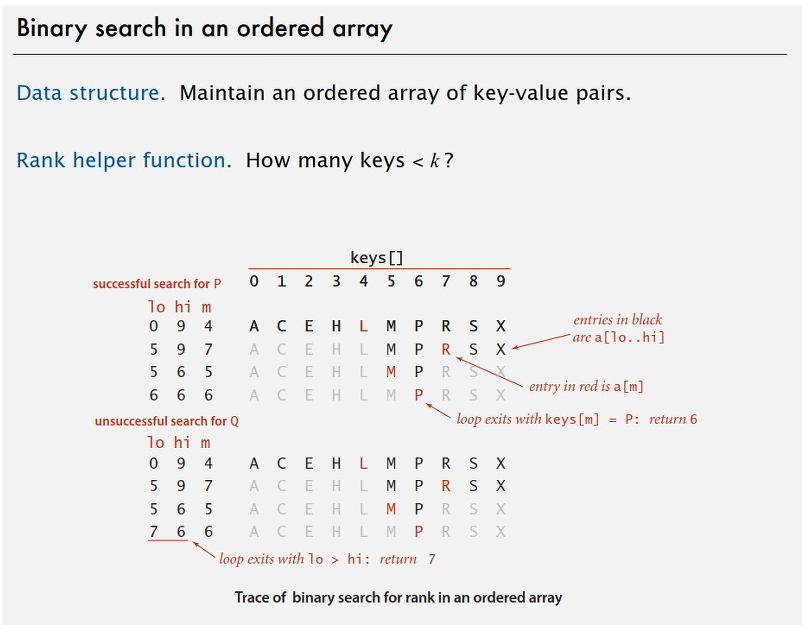
II-3. 이진 탐색 구현하기
중간 값 정하기, 범위 재 설정하기, 종료 조건 정하기
int rank(Key key) {
int lo = 0, hi = N-1;
while(lo <= hi) {
int mid = lo + (hi - lo) / 2;
if(key < keys[mid])
hi = mid - 1;
else if (key > keys[mid])
lo = mid + 1;
else
return mid;
}
return lo;
}III. Ordered Operations
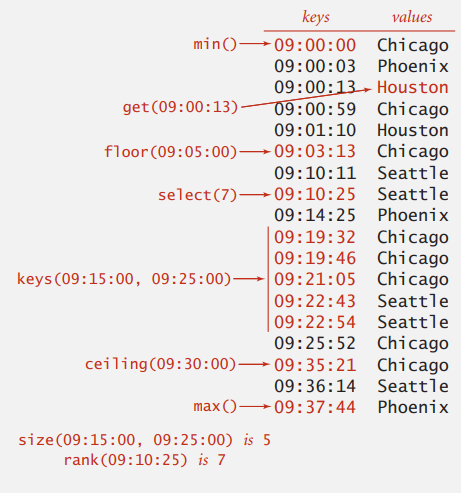
정렬된 상태의 자료 구조는 편리한 메서드를 구현할 수 있습니다.
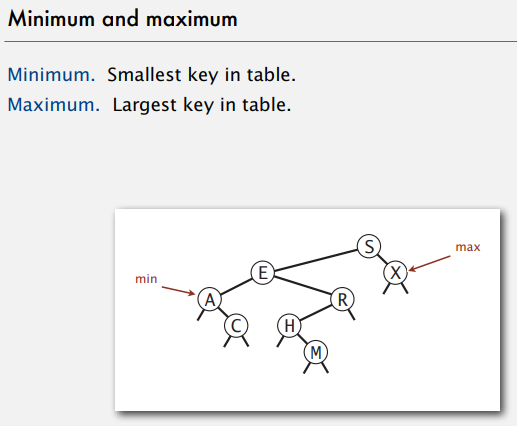
- 가장 작은 key를 가진 value는?
- 가장 큰 key를 가진 value는?
key1과key2사이의 key를 가진 value를 순환하는 방법?
IV. 이진 탐색 트리 (Binary Search Trees)
이진 탐색 트리는 다른 자료구조와 동일하게 자료를 담는 컨테이너지만, 자료를 정렬한 상태로 저장할 수 있습니다. 앞에서 설명한 것처럼 이진 탐색 트리는 이 점을 이용해 원소의 추가, 삭제와 같은 연산을 빠르게 수행합니다.
- 사용자 ID와 정보를 대응시키는 사전 객체 만들기
- 모든 학생들의 시험 점수를 저장하고, 나보다 1등 위인 사람과 1등 아래인 사람 찾기
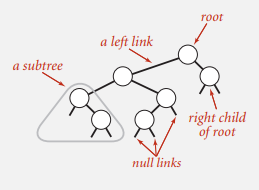
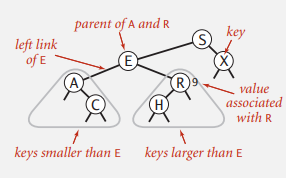
IV-1. 이진 탐색 트리의 정의
BST is a binary tree in symmetric order
- Binary tree: 각 노드가 왼쪽 (left), 오른쪽 (right) 최대 두 개의 자식 노드만을 가지는 트리
- Symmetric order: 왼쪽 서브트리에는 해당 노드보다 작은 노드만 들어가고, 오른쪽 서브트리에는 해당 노드보다 큰 노드만 들어가는 트리
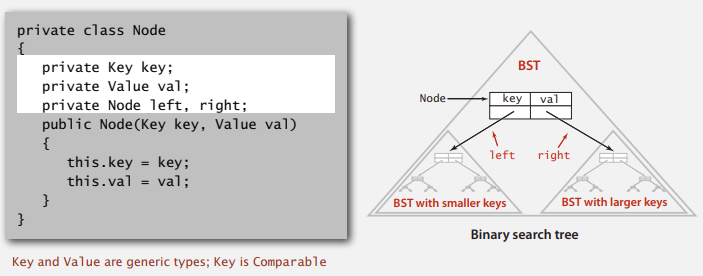
IV-2. 이진 탐색 트리 구현하기
Java에서 BST를 표현하는 방법은 연결 리스트와 동일하게 노드를 만들어서 정보를 저장하는 것입니다. 노드에는 저장할 key, value 값과 왼쪽 서브 트리의 left 노드, 오른쪽 서브 트리의 right노드를 저장하는 것만으로 트리 구조를 만들 수 있습니다.
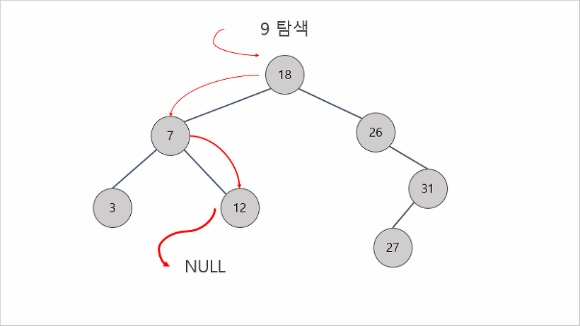
(a) 자료 탐색
이진 탐색과 비슷한 과정을 수행하지만, BST에서는 이미 left, right로 정렬되어 있다는 점이 다릅니다.

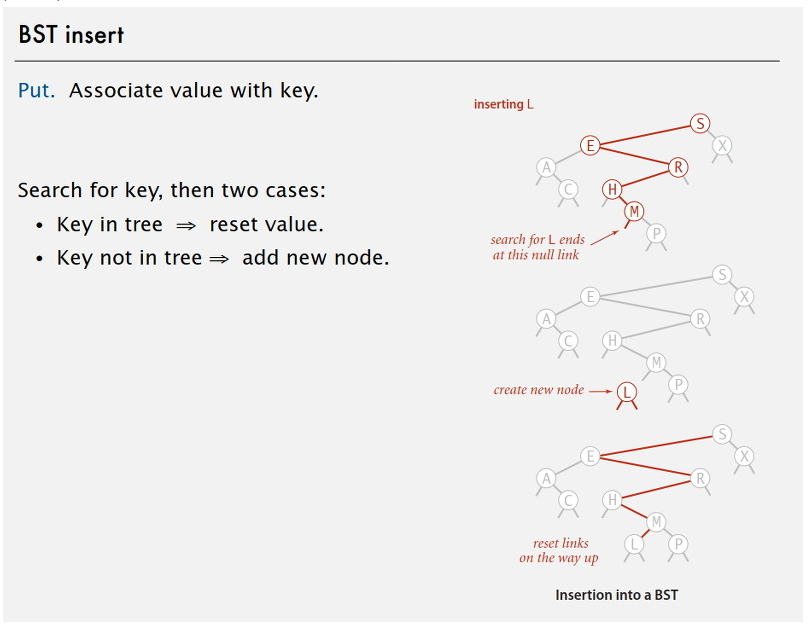
(b) 자료 삽입
- 자료를 탐색하다가 동일한 key가 존재하면 overwrite한다
- 탐색에 실패한 위치가 있으면 새로운 노드를 삽입한다
V. Ordered Operations in BSTs
VI. Deletion in BSTs
(c) 자료 삭제
이진 탐색 트리 관련 알고리즘 중 가장 복잡합니다. 먼저 삭제할 노드를 탐색합니다. 그리고 삭제할 노드를 찾았다면, 다음 세 가지 경우를 고려해야 합니다.
- 삭제하려는 노드의 자식 노드가 없을 때
- 삭제하려는 노드가 하나의 서브 트리만 가질 때
- 삭제하려는 노드가 두 개의 서브 트리를 모두 가질 때
(c)-1. 삭제하려는 노드의 자식 노드가 없을 때
- 해당 노드를 null로 만든다
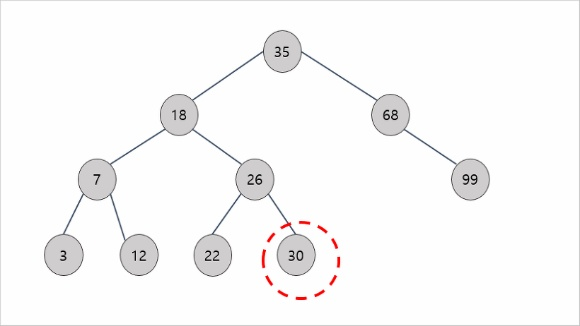
(c)-2. 삭제하려는 노드가 하나의 서브 트리만 가질 때
- 부모 노드에 서브 트리를 연결한다
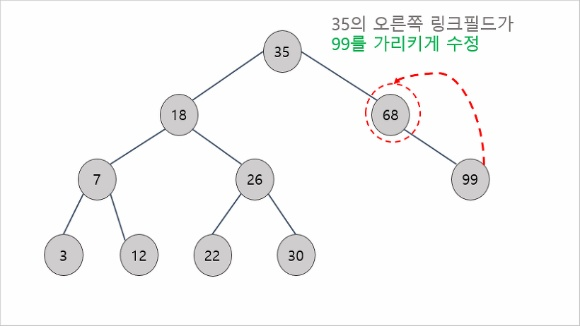
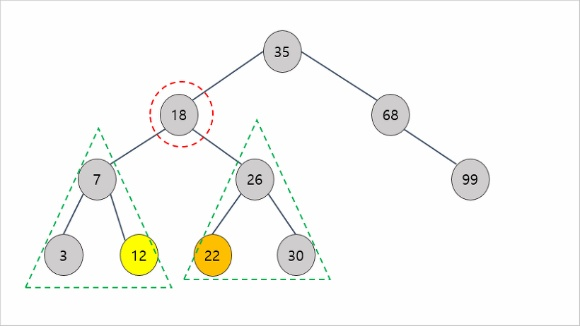
(c)-3. 삭제하려는 노드가 두 개의 서브 트리를 모두 가질 때
- 왼쪽 서브트리 중 가장 큰 노드를 삭제할 노드 위치와 바꾸거나
- 오른쪽 서브트리 중 가장 작은 노드를 삭제할 노드 위치와 바꾼다
'💻 programming > algorithm' 카테고리의 다른 글
| 퀵 소트 (Quicksort) - c/c++ (0) | 2021.05.05 |
|---|---|
| 기본 정렬 (Elementary Sort) (0) | 2021.02.26 |
| 최대 합 부분 배열 (Maximum sub-array problem) (0) | 2021.02.26 |



댓글